릿코드 62 unique-paths - Swift

https://leetcode.com/problems/unique-paths/

Unique Paths - LeetCode

 

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

 

Example 1:

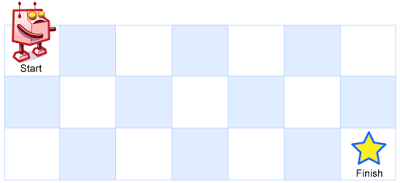
Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

 

Constraints:

• 1 <= m, n <= 100

 

풀이 방법

(0, 0) 에서 (m, n)으로 도달할 수 있는 방법의 수

모든 곳을 다 돌아야 하니까 DFS가 바로 떠올랐습니다. 테스트케이스에 대한 답이 2억 보다 작거나 같다고 하긴 했는데

시간에 대한 제약은 안 써있어서 DFS로 풀어봤습니다.

class Solution {
    func uniquePaths(_ m: Int, _ n: Int) -> Int {
        var queue = [(0, 0)]
        var index = 0
        var dx = [0, 1] // 아래, 오른쪽
        var dy = [1, 0]
        var answer = 0

        while index < queue.count {
            var node = queue[index]
            index += 1

            if node == (m-1, n-1) {
                answer += 1
                continue
            }

            for i in 0..<dx.count {
                var nextX = node.0 + dx[i]
                var nextY = node.1 + dy[i]

                if nextX < 0 || nextX >= m || nextY < 0 || nextY >= n {
                    continue
                } else {
                    queue.append((nextX, nextY))
                }
            }
        }

        return answer
    }
}

시간초과 났습니다.

그래서 DP를 생각했고 규칙을 파악하기 해당 좌표의 고유한 길의 갯수를 2차원 배열로 그려봤습니다.

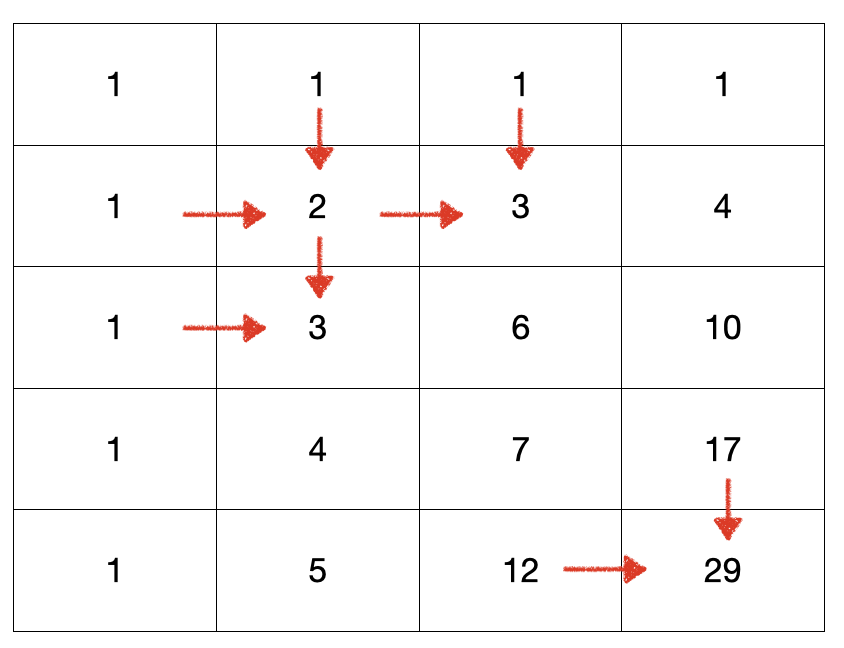
위 아래 더한 것이 자신의 되는 규칙을 확인하였습니다.

 

코드

class Solution {
    func uniquePaths(_ m: Int, _ n: Int) -> Int {
        var map = Array(repeating: Array(repeating: 0, count: n), count: m)
        
        for i in 0..<map.count {
            for j in 0..<map[0].count {
                if i == 0 || j == 0 {
                    map[i][j] = 1
                } else {
                    // 위, 왼쪽을 더한 것이 자신
                    map[i][j] = map[i-1][j] + map[i][j-1]
                }
            }
        }
        
        return map[m-1][n-1]
    }
}